#encoding=utf-8
import matplotlib.pyplot as plt
import numpy as np
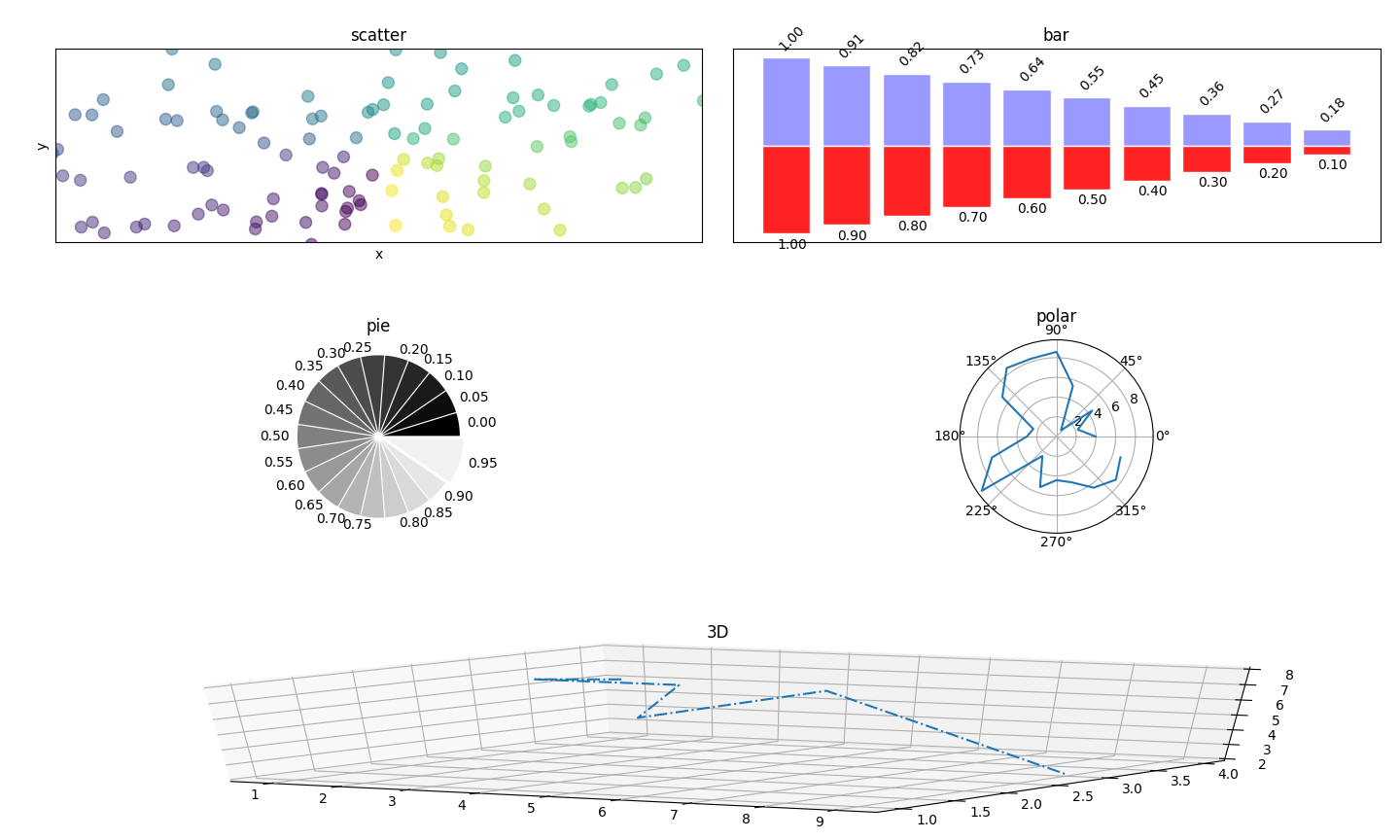
#散点图
fig=plt.figure()#画布
ax=fig.add_subplot(3,2,1)#3行3列第一个
n=128
X=np.random.normal(0,1,n)#生成随机数 正态分布 [numpy.random.normal(loc=0.0, scale=1.0, size=None)] 运行代码中 0->此概率分布的均值(对应着整个分布的中心centre) 1->此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)n->输出的shape,默认为None,只输出一个值
Y=np.random.normal(0,1,n)
T=np.arctan2(X,Y)
#print X,Y,T
#plt.axes([0.025,0.025,0.95,0.95])#对画图区域设置 axes([x,y,xs,ys])#其中x代表在X轴的位置,y代表在Y轴的位置,xs代表在X轴上向右延展的范围大小,ys代表在Y轴中向上延展的范围大小
ax.scatter(X,Y,s=75,c=T,alpha=0.5)#绘制散点图size color alpha
plt.xlim(-1.5,1.5),plt.xticks([])#x轴范围 不显示坐标轴刻度
plt.ylim(-1.5,1.5),plt.yticks([])
plt.axis()#显示轴
plt.title("scatter")
plt.xlabel("x")
plt.ylabel("y")
#柱状图
ax=fig.add_subplot(322)
n=10
X=np.arange(n)
Y1=(1-X/float(n+1))
Y2=(1-X/float(n))
#print X,Y1,Y2
ax.bar(X,+Y1,facecolor="#9999FF",edgecolor="white")
ax.bar(X,-Y2,facecolor="#FF2222",edgecolor="white")
for x,y in zip(X,Y1):
plt.text(x+0.1,+y+0.05,"%.2f"%y,ha="center",va="bottom",rotation="45")#bottom是柱状图相对于所标数字的位置
for x,y in zip(X,Y2):
plt.text(x+0.1,-y-0.05,"%.2f"%y,ha="center",va="top")
plt.title("bar")
plt.yticks([])
plt.xticks([])
#饼图
ax=fig.add_subplot(323)
n=20
Z=np.ones(n)
Z[-1]*=2
ax.pie(Z,explode=Z*0.05,colors=["%f"%(i/float(n)) for i in range(n)],labels=["%.2f"%(i/float(n)) for i in range(n)])
plt.gca().set_aspect("equal")
plt.xticks([])
plt.yticks([])
plt.title("pie")
#极坐标图
fig.add_subplot(324,polar=True)
n=20
t=np.arange(0.0,2*np.pi,2*np.pi/n)
r=10*np.random.rand(n)
plt.polar(t,r)
plt.title("polar")
#3D
from mpl_toolkits.mplot3d import Axes3D
fig.add_subplot(313,projection="3d")
plt.plot([1,3,5,6,7,9],[4,2,2,1,2,3],[6,8,8,7,8,2],linestyle="-.")
plt.title("3D")
#plt.savefig("./fig.png")#保存
plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0)#参数图像边界和子图之间的额外边距。边距以字体大小单位规定。
plt.show()